Wikipedia

Archivo:ExpIPi.gif

ExpIPi.gif (360 × 323 píxeles; tamaño de archivo: 11 kB; tipo MIME: image/gif, bucleado, 9 frames, 4,5s)

Este es un archivo de Wikimedia Commons, un depósito de contenido libre hospedado por la Fundación Wikimedia. Más abajo se reproduce su página de descripción con la información sobre su origen y licencia.

Resumen

Descripción This is a demonstration that Exp(i*Pi)=-1 (called Euler's formula, or Euler's identity). It uses the formula (1+z/N)^N --> Exp(z) (as N increases). The Nth power is displayed as a repeated multiplication in the complex plane. As N increases, you can see that the final result (the last point) approaches -1, the actual value of Exp(i*pi).
Fecha
Fuente Trabajo propio
 
Este diagrama fue creado con Mathematica por n
Autor Sbyrnes321

Licencia

Public domain Yo, el titular de los derechos de autor de esta obra, lo libero al dominio público. Esto aplica en todo el mundo.
En algunos países esto puede no ser legalmente factible; si ello ocurriese:
Concedo a cualquier persona el derecho de usar este trabajo para cualquier propósito, sin ningún tipo de condición al menos que éstas sean requeridas por la ley. 
(* Source code written in Mathematica 6.0, by Steve Byrnes, 2008. I release this code into the public domain. *)

plot1 = Table[
  ListPlot[Table[{Re[(1 + (\[ImaginaryI] \[Pi])/n)^m], 
     Im[(1 + (\[ImaginaryI] \[Pi])/n)^m]}, {m, 0, n}], 
   PlotJoined -> True, PlotMarkers -> Automatic, 
   PlotRange -> {{-2.5, 1.1}, {0, \[Pi] + .05}}, AxesOrigin -> {0, 0},
    AxesLabel -> {"Real part", "Imaginary part"}, 
   PlotLabel -> "N = " <> ToString[n], 
   AspectRatio -> Automatic], {n, {1, 2, 3, 4, 5, 10, 20, 50, 100}}];

Export["ExpIPi.gif", plot1, "DisplayDurations" -> {2}, 
 "AnimationRepititions" -> Infinity ]

Leyendas

Añade una explicación corta acerca de lo que representa este archivo

Elementos representados en este archivo

representa a

Historial del archivo

Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.

Fecha y horaMiniaturaDimensionesUsuarioComentario
actual19:46 25 mar 2010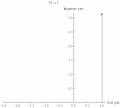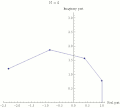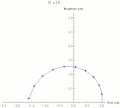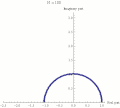Miniatura de la versión del 19:46 25 mar 2010360 × 323 (11 kB)Aiyizooptimized animation, converted to 16 color mode
17:19 5 may 2008Miniatura de la versión del 17:19 5 may 2008360 × 323 (20 kB)Sbyrnes321{{Information |Description=This is a demonstration that Exp(I*Pi)=-1 (called Euler's formula, or Euler's identity). It uses the formula (1+z/N)^N --> Exp(z) (as N increases). The Nth power is displayed as a repeated multiplication in the complex plane. As
16:58 5 may 2008Miniatura de la versión del 16:58 5 may 2008360 × 308 (18 kB)Sbyrnes321{{Information |Description=This is a demonstration that Exp(I*Pi)=-1 (called Euler's formula, or Euler's identity). It uses the formula (1+z/N)^N --> Exp(z) (as N increases). The Nth power is displayed as a repeated multiplication in the complex plane. As

La siguiente página usa este archivo:

Uso global del archivo

Las wikis siguientes utilizan este archivo:

Obtenido de «https://es.wikipedia.org/wiki/Archivo:ExpIPi.gif»