Resonance frequency

Question

How does one find the resonance frequency in a circuit?

Wikipedia and the like give some definitions that are not very useful in practice. I found somewhere(I think on this site but I cannot find it anymore) a definition that said that the resonance frequency is when the impedance is purely real. This made intuitively sense and worked in many cases but I ran into trouble with this circuit:

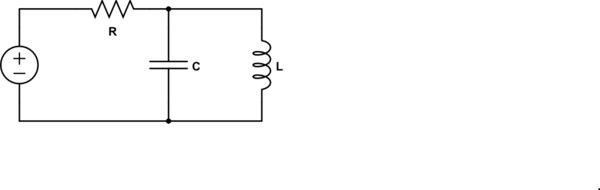
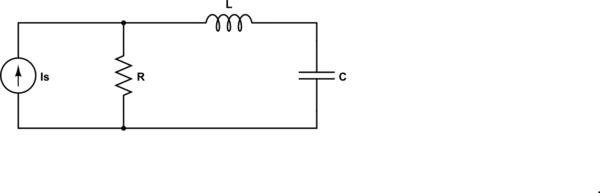
^{simulate this circuit – Schematic created using CircuitLab}

I found the impedance of this circuit to be:

$$ Z = R + \frac{1}{\frac{1}{j\omega L} +j\omega C}=R + \frac{j\omega L}{1-\omega^2 LC} $$ Setting the imaginary part to zero I get \$\omega = 0\$, but I think that in this case, it should corresponds to \$\omega = \frac{1}{\sqrt{LC}}\$ which makes the imaginary part infinite and the transfer function 1.

So is that correct and if so how do you find the resonance in general?

EDIT: My question is

Since the above definition for resonance does NOT work in the circuit above, what is the correct one? and HOW do you find the resonance for a given circuit?

EDIT 2

I am considering IDEAL elements only.

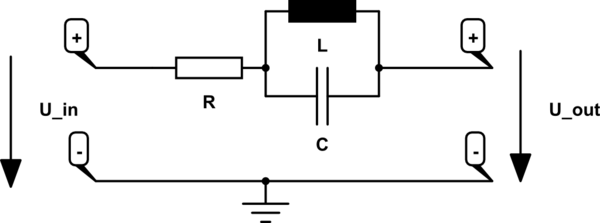
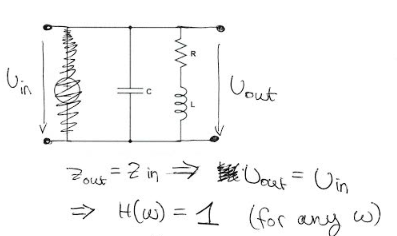
Consider another circuit:

^{simulate this circuit}

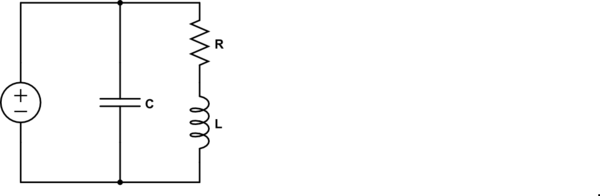
$$ Z = \frac{R+j\omega L}{1+Rj\omega C -\omega^2LC} $$ The resonance frequency for this circuit is $$ \omega_0 = \sqrt{\frac{1}{LC} -\frac{R^2}{L^2}} $$ which is obtained by using the method I outlined initially(setting imaginary part of Z to 0). This frequency is neither a pole or a zero of the impedance. Rather, $$ Z(\omega_0) = \frac{L}{RC} $$ Also, the impedance of the inductor and capacitor are not equal in magnitude.

So I still don't know how to find the frequency in general.

Answer 1

Your calculation of the impedance seen by the source is correct.

Clearly, there is a 'special' (angular) frequency

$$\omega_0 = \frac{1}{\sqrt{LC}}$$

where there is a pole in the impedance - the impedance goes to infinity.

Now, let's look at the dual of the circuit given:

^{simulate this circuit – Schematic created using CircuitLab}

For the dual circuit, the impedance seen by the source is

$$Z = R||(j\omega L + \frac{1}{j \omega C}) = R \frac{1 - \omega^2LC}{1 - \omega^2LC + j\omega RC} $$

and now we have a zero at \$\omega_0\$ - the impedance goes to zero.

In both of these cases, the pole or zero is on the \$j \omega\$ axis. Generally, they are not.

so how do you find the resonance in general?

In this context (RLC), the resonance frequency is the frequency where the impedance of the inductor and capacitor are equal in magnitude and opposite in sign.

---

Update to address comment and question edit.

From the Wikipedia article "RLC circuit", "Natural frequency" section:

The resonance frequency is defined in terms of the impedance presented to a driving source. It is still possible for the circuit to carry on oscillating (for a time) after the driving source has been removed or it is subjected to a step in voltage (including a step down to zero). This is similar to the way that a tuning fork will carry on ringing after it has been struck, and the effect is often called ringing. This effect is the peak natural resonance frequency of the circuit and in general is not exactly the same as the driven resonance frequency, although the two will usually be quite close to each other. Various terms are used by different authors to distinguish the two, but resonance frequency unqualified usually means the driven resonance frequency. The driven frequency may be called the undamped resonance frequency or undamped natural frequency and the peak frequency may be called the damped resonance frequency or the damped natural frequency. The reason for this terminology is that the driven resonance frequency in a series or parallel resonant circuit has the value1

$$\omega_0 = \frac {1}{\sqrt {LC}}$$

This is exactly the same as the resonance frequency of an LC circuit, that is, one with no resistor present, that is, it is the same as a circuit in which there is no damping, hence undamped resonance frequency. The peak resonance frequency, on the other hand, depends on the value of the resistor and is described as the damped resonance frequency. A highly damped circuit will fail to resonate at all when not driven. A circuit with a value of resistor that causes it to be just on the edge of ringing is called critically damped. Either side of critically damped are described as underdamped (ringing happens) and overdamped (ringing is suppressed).

Circuits with topologies more complex than straightforward series or parallel (some examples described later in the article) have a driven resonance frequency that deviates from \$\omega_0 = \frac {1}{\sqrt {LC}}\$ and for those the undamped resonance frequency, damped resonance frequency and driven resonance frequency can all be different.

See the "Other configurations" section for your 2nd circuit.

In summary, the frequencies at which the impedance is real, at which the impedance is stationary (max or min), and at which the reactances of the L & C are equal can be the same or different and each is some type of resonance frequency.

Answer 2

Resonance frequency for sure will be

\$\omega = \frac{1}{\sqrt{LC}}\$ [rad/s]

or

\$f = \frac{1}{2\pi\sqrt{LC}}\$ [Hz]

Your formula for Z must be wrong. You should end up with something like this:

Impedance is:

\$Z(\omega) = -j \frac{ \omega L}{\omega^{2}LC-1} + R\$

Maybe forget complex numbers, it should be easier with reactances \$Xl\$ and \$Xc\$. We can do that because we considering this as ideal coil and capacitor (vector angles are -90 and +90).

Resonance happends when \$Xl = Xc\$. Impedance vectors for ideal coil and capacitor are opposite so they substract and that makes impedance vector equal zero.

\$Xc = \frac{1}{2\pi{fC}}\$

\$Xl = {2\pi{fL}}\$

so need to find f here:

\${2\pi{fL}} = \frac{1}{2\pi{fC}}\$

with omega will be easier

\${\omega{L}} = \frac{1}{\omega{C}}\$

\${\omega{L}} * {\omega{C}} = 1\$

\${\omega\omega{LC}} = 1\$ (i have no idea how to make power here)

... (I will short this, this syntax is not friendly to transform formulas "on the fly"

\$\omega = \frac{1}{\sqrt{LC}}\$ [rad/s]

I've made a picture for better understanding of resonance:

So if resonance happends - in hypotetical ideal LC circuit there are no power losses on reactance. Energy flows from coil (magnetic field) to capacitor (electric field) and it flows back and forth with resonance frequency.

In real life some current cause thermal losses on coil windings. In capacitor some electric field is discharged by resistance between capacitor electrodes. These losses are not affecting resonance frequency but there are some other parasitic losses (inductance in capacitor, capacity in coil etc.), capacity and inductance changes due changes to environment (temperature, magnetic permeability of coil neigbourhood and they may change resonance frequency a bit.

Answer 3

The reason you are having trouble is because setting the imaginary part of the impedance to zero to find the resonant frequency only works for series rlc circuits. For parallel circuits, if there is resistance in the circuit resonance occurs where the impedance is maximum, and resonance occurs when the admittance has zero imaginary part.

When you have an ideal inductor and an ideal capacitor in parallel, the resonant angular frequency is simply \$\frac{1}{\sqrt{LC}}\$. When there is resistance in series with the inductor or capacitor, it is as if these components are non ideal, and the above equation no longer gives the frequency of maximum amplitude.

Answer 4

You derived this correctly: -

\$Z = =R + \dfrac{j\omega L}{1-\omega^2 LC}\$

Now what condition would arise that would make the impedance infinite?

It can only be when the denominator equals zero therefore: -

\$1-\omega^2 LC\$ = 0 and rearranging, \$\omega = \dfrac{1}{\sqrt{LC}}\$

For the 2nd part of the question (non-ideal inductor) you have a formula for omega when the impedance of the RLC circuit is purely real i.e. no imaginary part to the impedance. I'll attempt to prove that: -

Z = \$\dfrac{R+j\omega L}{1+j\omega CR -\omega^2LC}\$.

You need to make the denominator real by multiplying top and bottom with the denominator's complex conjugate. Then you can ignore the denominator because it's real. The numerator becomes: -

\$(R+j\omega L)\cdot(1-j\omega CR -\omega^2LC)\$ - note the \$j\omega CR\$ term is now negative.

Multiplying out we get: -

\$R - j\omega CR^2 - \omega^2 LCR + j\omega L -j^2\omega^2 LCR - j\omega^3 L^2C\$

Now, equate the imaginary parts to zero: -

\$0 = -\omega CR^2 + \omega L - \omega^3 L^2 C\$ and divide thru by omega to get

\$\omega^2 L^2 C + CR^2 = L \$ and therefore

\$\omega^2 = \dfrac{L}{L^2 C} - \dfrac{CR^2}{L^2 C}\$ which means \$\omega = \sqrt{\dfrac{1}{LC} - \dfrac{R^2}{L^2}}\$

If you were to calculate where the pole is (irrespective of the complexity of the impedance it's simpler - you need to equate the denominator to zero and use the solution to a quadratic equation to find the complex s value. Denominator is: -

\$s^2 + s\dfrac{R}{L} + \dfrac{1}{LC}\$

Therefore s = \$\dfrac{-\dfrac{R}{L}}{2} +/-\sqrt{\dfrac{R^2}{4L^2}-\dfrac{1}{LC}}\$

To get the complex nature of s you negate the part under the square root sign and bring \$\sqrt{-1}\$ outside to form the "j" operator: -

\$j\omega = +/-j\sqrt{\dfrac{1}{LC}-\dfrac{R^2}{4L^2}}\$

This second part of the equation is on the jw axis and represents where the pole's co-ordinate would be along that axis. The first part of the above equation is the real part of s in the pole-zero diagram.

Conclusion - there are two important frequencies in the case of the lossy inductor parallel resonated with a capacitor - how do you learn to get from A to B. Sometimes it's a real battle and you just have to dig a little deeper. I say there's two frequencies but in fact there is another frequency that is important - the 3dB roll-off point but I'm not going there today.

Answer 5

This is a circuit in which the LC "antiresonates" -- at some frequency the combined impedance is infinite (or in a practical circuit, at least maximum). This configuration is used for tuning in AM radio and elsewhere-- as you noted the transfer function becomes 1 at the resonant frequency.

Answer 6

I had the same problem with the resonance freqency. When I asked someone for a general method of finding the resonance frequency of a cirquit, I was told to use the transfer function instead of the impedance accross the circuit.

If we want to use the transferr function, we need 4 nodes (2 for the input and 2 for the output). This makes sense, because the phase shift of a signal is equal to zero at resonance and a signal's phase shift can't be evaluated unless the original signal and the shifted (output) signal are known.

Now that I have an input and output signal/impedance, I can find the imaginary part of my transfer function and set it to zero. After setting the imaginary part of the transfer function to zero, I just solve for omega, and it turns out that this method works for the bandpass filter that was posted in the original question.

Again, it intuitively makes sense that the imaginary part of the transfer function should be set to zero because the transfer function compares the input against the output of a circuit.

If I define U_out like this:

^{simulate this circuit – Schematic created using CircuitLab}

Effectively we just converted the original problem (without a transfer function) into a problem with a transfer function. Clearly this is not a band pass filter, if anything it's a band stop filter.

In this problem, I can show that the transfer function is equal to the impedance of the original circuit: $$ U_{out} = U_{in}\cdot(R + (Z_L || Z_C)) \Rightarrow H(\omega) = \frac{U_{out}}{U_{in}} = R + (Z_L || Z_C) = Z_{ofTheFirstCircuit} $$

so as long as the resonance frequency of this new circuit is the intended resonance frequency, it should be safe to do the calculation with the impedance rather than the transfer function. Best is to just stick with the transfer function and be sure that

As always, in the end this always applies: $$ \phi = arctan(\frac{Im(Z)}{Re(Z)}) \Rightarrow Im(Z) = 0, \phi = 0 $$ Where Z is the transfer function (regardless of whether it's equal to the impedance or not).

I hope this solves our problem. I haven't tested it on any other circuits yet so I can't guarantee that it always works, but for now I am happy with this method and I don't see any situation where it doesn't work.

Note:

$$ Where\: \omega \ne \infty $$

In this case there is no phase shift.

Answer 7

Since in parallel circuit imaginary part of admittance should be zero not that of impedance....which is required for a maximum value of voltage.whereas current should be maximum in series resonant circuit for a constant value of voltage...so here imaginary part of 'impedance'should be zero.