Damcaniaeth graffiau
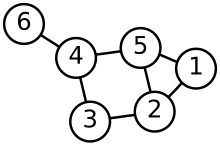
Mewn mathemateg a gwyddoniaeth gyfrifiadurol, astudiaeth o graffiau yw damcaniaeth graffiau. Set o fertigau, nodau neu bwyntiau wedi'u cysylltu gan ymylon, arcau neu linellau yw "graff" yn y cyd-destyn hwn, ac ni ddylid ei ddrysu gyda'r "graff" sy'n perthyn i ffwythiant.
Hanes
[golygu | golygu cod]Mae'n debyg mae'r papur a sgrifennwyd gan Leonhard Euler am Saith Pont Königsberg ym 1736 oedd y cyntaf a gyhoeddwyd ynglŷn â damcaniaeth graffiau. Roedd y cyhoeddiad hwn, a phapur Vandermonde am broblem y marchog yn datblygu ymhellach yr analysis situs a gychwynwyd gan Leibniz.
Ymysg y mathemategwyr enwog oedd yn weithgar ar broblemau damcaniaeth graffiau yn y canrifoedd canlynol oedd Cauchy, L'Huillier, Arthur Cayley, George Pólya, a Nicolaas Govert de Bruijn. Bathwyd y term graph (yn ein ystyr ni) ym 1878 gan Sylvester.
Un o'r problemau enwocaf yn hanes damcaniaeth graffiau yw'r problem pedwar lliw. Lluniwyd y broblem gan Francis Guthrie ym 1852 hyd a wyddys. Ni lwyddodd neb i brofi'r ddamcaniaeth am dros ganrif, er i Cayley, Kempe ac eraill cynhyrchu profion gwallus. Fe gyhoeddodd Kenneth Appel a Wolfgang Haken prawf ohoni ym 1976, ond ni argyhoeddwyd pawb yn y gymuned fathemategol ohono, am ei fod yn ddibynnol ar defnydd o gyfrifiadur i wirio 1936 o achosion arbennig. Rhoddwyd prwawf symlach, a ystyrir yn ddilys gan bawb mwy neu lai, gan Robertson, Seymour, Sanders and Thomas ym 1997.
Roedd y broblem pedwar lliw yn ysbrydolaeth astudiaeth o lliwio graffiau ar wynebau o wahanol genws gan Tait, Heawood, Frank P. Ramsey, Hugo Hadwiger, Julius Petersen, Pál Turán ac eraill.
Bu datblygiad annibynnol topoleg rhwng 1860 a 1930 cyfranu'n ffrwythlon iawn i damcaniaeth graffiau trwy weithiau Jordan, Kuratowski a Hassler Whitney. Bu datblygiad algebra haniaethol yn ddefnyddiol hefyd, ac roedd profi rheolau cylchred Kirchhoff yn enghraifft cynnar o hynny.
Cyflwynwyd dulliau tebygolrwydd mewn damcaniaeth graffiau gan Erdős ac Rényi, a arweiniodd at astudiaeth o hap-graffiau.